Paack delivers parcels to online customers in the most convenient and sustainable manner. In line with our Sustainability goals, we aim at operating in the most efficient manner by, for instance, minimizing the number of vehicles on the road and their overall distances travelled while ensuring the high service levels that Paack is committed to offer. The optimization of the line-haul (middle-mile) transportation network is part of those goals.
Designing the optimal middle mile line-haul network

The line-haul network is designed to transport parcels from origins (cross-dock WH) to destinations (last-mile WHs) while respecting hard time windows for both the departure and arrival of parcels. The picture on the left shows the nodes (warehouses) of a very simple network, which includes a unique cross-dock WH (square) and seven last-mile destinations (circles).
(!) Keep in mind that this is just a theoretical case.
When designing the line-haul network, several questions arise:
- Shall we run direct lines?
- Is it time-wise feasible to do milk-runs?
- Which last-mile destinations should be connected via common transport lines?
- What vehicle type should we contract for each line?
The number of possible combinations of routes and vehicle types is just way too large for them to be computed and evaluated manually to then select the best one.
Using optimization techniques from the field of Operations Research, we are able to find the optimal solution for such highly complex decision-making problems where the number of possible solutions is exponentially large, in an automated way!
By formulating the problem mathematically, powerful solution search engines (called “solvers”) are able to search the solution space in an intelligent way and output the mathematically proven optimal solution, i.e., the best out of possibly millions of combinations, which would otherwise hardly be found. Not only we let the computer do the tedious work of finding and evaluating new solutions, but we are also able to find the very best one of all in a very quick way! Here is how it is done:
In our example network, by using the coordinates of the involved facilities we are able to compute the road distances between every pair of nodes via requests made to a web mapping platform. Average traffic conditions and road closures are considered in this calculation.
Population data may also be used to estimate the percentage of the total volume (in pallets) that will be transported from the cross-dock center to each last-mile destination, when historical data is not available. There are several vehicle types that can be contracted to perform the transport of parcels, from a Luton van to a semi-truck or a full trailer.
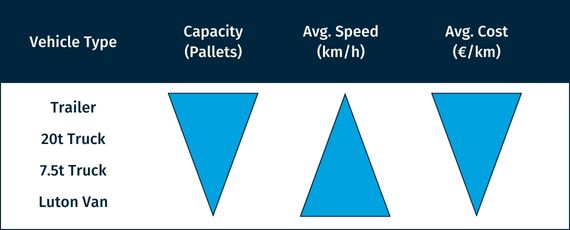
As shown in the table above, larger vehicles have more carrying capacity (and thus have a lower cost per parcel when full) but are typically slower. This tradeoff between speed and cost is implicit in the optimization model.
Mathematical optimization model
Optimization models allow to mathematically formulate a certain decision problem by means of decision variables, whose values will be selected such as to minimize (or maximize) an objective function and bounded by a system of linear equations representing the real-world constraints for that decision problem. In our line-haul optimizer:
Decision variables – each of the variables X must take the value 0 or 1 in a feasible solution (integer programming), leading to thousands of possible combinations (only a subgroup of those represent a feasible solution though).
Objective function – function that guides the solution search process, i.e. decides the direction of the optimization and whether a newly encountered feasible solution is better than the previous one or not.
Constraints – linear equations that bound the possible values of our decision variables. Constraints ensure that the solution to be implemented is feasible regarding the real problem, and therefore must ensure that:
- All parcels are picked up and delivered within the pre-defined time windows
- Capacity constraints of the vehicles contracted are respected
- Warehouse opening times are respected
- …
In total, there are currently 16 groups of constraints in our optimization model!
Optimal line-haul network
The mathematical model and input data are then used together with a solver, an algorithm capable of finding the optimal solution for integer programming problems in a matter of seconds (for this simple network). The optimal solution is then used to generate a graph (networkX python package) depicting the active connections colored by vehicle type and containing the estimated time of departure and arrival from and to each node. Metrics per line and per destination are also computed to the user.
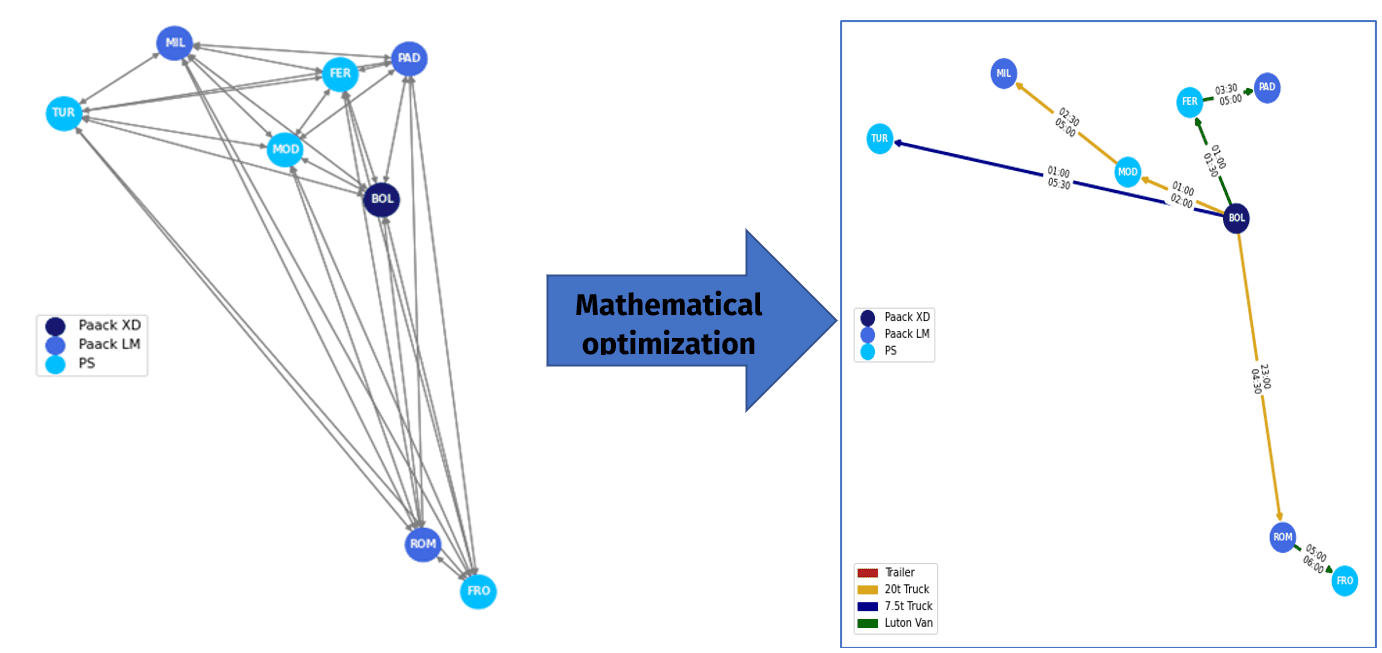
For larger computational problems such as the ones encountered in our actual daily operations, unreasonably longer computational times may be needed to achieve optimality. In these cases, the problem is usually reduced in dimension by splitting it into smaller problems, or by cutting out possible combinations “a priori” via additional constraints or input data manipulation.
Sensitivity analysis
By changing some input parameters and re-running the model we are able to find and quantify potential improvements in the network. In this example, by anticipating the pick-up time at the cross-dock warehouse by 2 hours a cost decrease of 11% could be achieved, as more volume could be consolidated in a larger vehicle at a lower cost!

The optimization of the line-haul network for Paack’s middle-mile transportation brings several benefits apart from reducing transportation costs directly. It allows for the design of more reliable transport planning with increased dispatch time compliance and, consequently, increased service levels for the convenience of our costumers. Optimized transport networks also lead to more sustainable deliveries by reducing the number of vehicles on the road and the overall distances travelled when compared to manually built solutions.