En línea con nuestros objetivos de sostenibilidad, queremos operar y entregar pedidos de la manera más eficiente y sostenible posible. Para ello, minimizamos el número de vehículos en carretera y las distancias totales que recorren, sin poner en riesgo la calidad del servicio que Paack se compromete a ofrecer. La optimización de la red de line-hauls (transporte de media milla) también forma parte de estas acciones a favor de una logística más sostenible.
Diseñando la red de media milla óptima
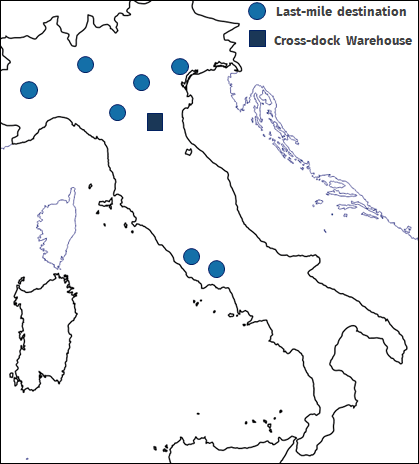
La red line-haul está diseñada para transportar paquetes desde su origen (WH de crossdock) hasta sus destinos (WH de última milla) respetando las franjas horarias específicas tanto para llegadas como salidas de paquetes. La imagen de la izquierda muestra los nodos (warehouses) de una red muy simple, que incluye un único WH crossdock (cuadrado) y siete destinaciones de última milla (círculos).
(!) Ten en cuenta que este es solamente un caso teórico.
Al diseñar una red line-haul, surgen distintas preguntas:
- ¿Deberíamos planificar líneas directas a cada destino?
- ¿Es factible en términos de tiempo efectuar milk-runs?
- ¿Qué destinaciones de última milla deberían estar conectadas a través de líneas de transporte comunes?
- ¿Qué tipo de vehículo deberíamos contractar para cada línea?
El número de combinaciones de rutas y de tipos de vehículos es demasiado extenso para computarlos, evaluarlos manualmente y, luego escoger la mejor solución.
Gracias a técnicas de optimización de Investigación Operativa, es posible encontrar la planificación óptima para solucionar la toma de decisiones con problemas tan complejos de forma automatizada, donde el número de posibles soluciones es exponencialmente alto.
Al formular el problema matemáticamente, potentes sistemas de búsqueda de soluciones (llamados “solucionadores”) son capaces de buscar y encontrar de forma inteligente la solución óptima (desde el punto de vista matemático), que de otra forma sería realmente compleja de obtener. No solo dejamos que el ordenador haga la tediosa tarea de encontrar y evaluar nuevas soluciones, sino que además también somos capaces de conseguir la mejor de todas de forma muy rápida. Así es como lo hacemos:
En nuestro ejemplo, al usar las coordenadas de las instalaciones, somos capaces de calcular las distancias por carretera entre cada par de nodos a través de solicitudes hechas a una plataforma web de mapeo. En estos cálculos, se tienen en cuenta las condiciones de tráfico habitual y los cortes de carretera.
Siempre y cuando no tengamos datos históricos, se pueden usar también datos de población para estimar el porcentaje de volumen total (en pallets) que se transportará a cada destinación de última milla.
Hay varios tipos de vehículos con los que llevar a cabo el transporte de paquetes de media milla, desde una furgoneta hasta un minitir, o un tráiler entero.
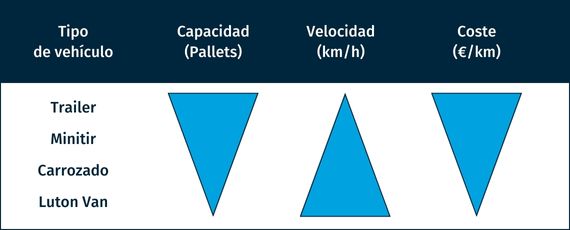
Los vehículos más grandes tienen más capacidad de carga (y, por lo tanto, un menor coste por paquete cuando se llena), pero normalmente son más lentos. Este intercambio entre velocidad y coste está implícito en el modelo de optimización.
Modelo de optimización matemático
Los modelos de optimización permiten formular matemáticamente un determinado problema de decisión por medio de variables de decisión, cuyos valores serán seleccionados de forma a minimizar (o maximizar) una determinada función objetivo, y serán elegidos también de forma a satisfacer un conjunto de ecuaciones lineales que representan las restricciones operacionales del problema real. En nuestro ejemplo:
Variables de decisión – Cada una de las variables X debe tener un valor entre 0 y 1 (programación binaria o entera), lo que nos lleva a miles de posibles combinaciones (sin embargo, solo un subgrupo de esas representa una solución factible).
Función objetivo – La función que guía el proceso de búsqueda de soluciones, que decide si una nueva solución factible encontrada es mejor que la anterior mejor o no.
Restricciones – ecuaciones lineares que limitan los posibles valores de nuestras variables de decisión. Las restricciones garantizan que la solución a implementar sea factible respecto al problema real, por lo que deben asegurar que:
- Todos los paquetes se recogen y entregan dentro de las ventanas de tiempo predefinidas
- Se respeten las restricciones de capacidad de los vehículos contratados
- Los horarios de los almacenes se respetan
- …
¡Actualmente, nuestro optimizador de line-hauls contiene más de 16 grupos de restricciones!
La red óptima de transporte de media milla
El modelo matemático y los datos de entrada se utilizan para esta red sencilla junto con un solucionador, un algoritmo capaz de encontrar la solución óptima para problemas de programación entera en cuestión de segundos. La solución óptima se utiliza entonces para generar un gráfico (paquete python networkX) que representa las conexiones activas coloreadas según el tipo de vehículo y que contiene la hora estimada de salida y llegada de cada nodo.
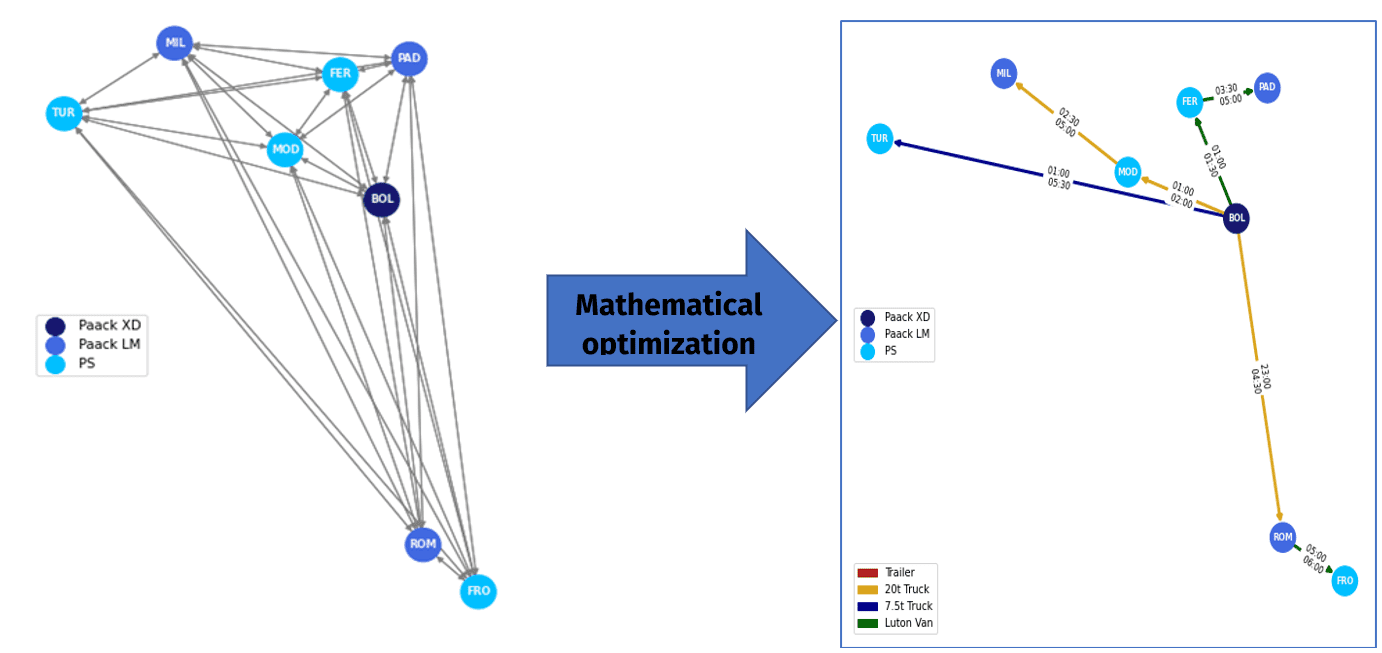
En el caso de los problemas computacionales de mayor envergadura, como los que encontramos en nuestras operaciones diarias, pueden ser necesarios tiempos de cálculo excesivamente largos para lograr concluir la optimización. En estos casos, se suele reducir la dimensión del problema dividiéndolo en subproblemas más pequeños, o recortando posibles combinaciones a priori mediante restricciones adicionales o reduciendo la dimensión del problema por medio de los datos de entrada.
Análisis de sensibilidad
Cambiando algunos parámetros de entrada y volviendo a ejecutar el modelo, podemos encontrar y cuantificar posibles mejoras en la red. En este ejemplo, si se anticipa el tiempo de recogida en el almacén de cross-dock en 2 horas, se puede conseguir una reducción de costes de transporte del 11%, ya que se puede consolidar más volumen en un vehículo más grande a un coste menor.
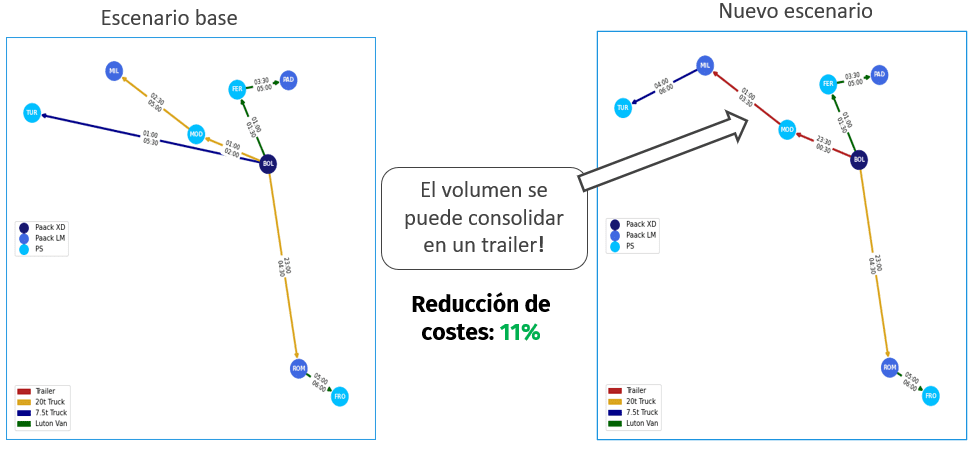
La optimización de la red de transporte de media milla de Paack aporta varios beneficios, además de reducir directamente los costes de transporte. Permite diseñar una planificación del transporte más fiable, con un mayor cumplimiento de los plazos de envío y, en consecuencia, un mayor nivel de servicio para comodidad de nuestros clientes. Las redes optimizadas también conducen a entregas más sostenibles al reducir el número de vehículos en la carretera y las distancias totales recorridas en comparación con las soluciones construidas manualmente.





